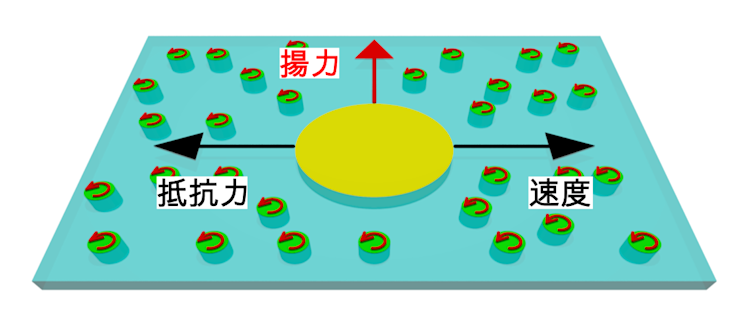
Hydrodynamics of an odd-viscous fluid:
We theoretically study transport phenomena in an active chiral fluid with a particular interest in odd viscosity, which features the breaking of the time-reversal and parity symmetries. We have obtained the Green's function and the resistance tensor of disk-shaped objects in 2D odd flows. More recently, we have been interested in active transport, such as dynamics of microswimmers, in active fluids characterized by odd viscosity, by generalizing the versatile hydrodynamic principle called the Lorentz reciprocal theorem with odd viscosity.
- Y. Hosaka, et al., Phys. Rev. Research (2024)
- Y. Hosaka, et al., Phys. Rev. Lett. (2023)
- Y. Hosaka, et al., New J. Phys. 25, 083046 (2023).
- Y. Hosaka, et al., Eur. Phys. J. E 46, 18 (2023)
- Y. Hosaka, et al., Biophys. Rev. Lett. 17, 51 (2022)
- Y. Hosaka, et al., Phys. Rev. E 104, 064613 (2021)
- Y. Hosaka, et al., Phys. Rev. E 103, 042610 (2021)

Active diffusion in a membrane:
Anomolous diffusion in biocells and membranes has been observed so far. Here we theoretically obtained the diffusion coefficient of the tracer in the 2D membrane where active force dipoles mimicking enzymes are present. The diffusion turned out to deviate from the thermal diffusion.
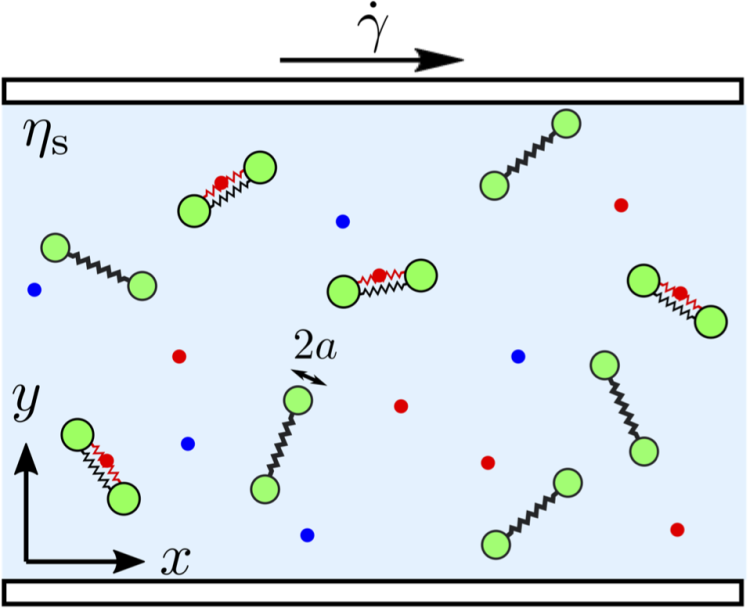
Rheological properties of an enzyme solution:
We study the rheological properties of an enzyme solution as it would be complementary to the exsting Microrheology, which investigates the local properties in cells or membranes